Polynomial Equations

Solving a polynomial equation can be done algebraically if it is factorable or graphically if it not. Note that a polynomial function is y = P(x) and a polynomial equation is when P(x) = 0. 


If the polynomial equation is factorable, the roots are determined by solving each factor when it is equal to zero. For example, 

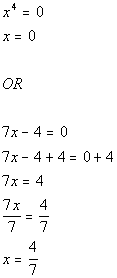
The x-intercepts of the graph are 0 and 4/7. The x-intercepts of a polynomial function graph correspond to the real roots of the polynomial equation P(x) = 0. Therefore, the roots for the polynomial equation in the example above is also 0 and 4/7.


P(x) can also be solved using the factor theorem. To solve the cubic x³ - x² + x -1 = 0,  
we first figure out the values that should be tested using the rational zero theorem. If P(x) is a polynomial function with integer coefficients and x = b/a is a zero of P(x), then b is a factor of the constant term while a is a factor of the leading coefficient. Furthermore, ax - b is a factor of P(x). Back to the equation, since a=1 and b=-1, the only possible values of b/a is 1. By substitution, we see that x=1 is a root thus (x-1) is a factor. We then find the other factor by dividing with (x-1) which produces the quotient x² +1. Thus, 

x³ - x² + x - 1 = (x - 1)(x² + 1) = 0

x - 1 = 0

x² + 1 = 0

Since a square root of a negative value is not a real number, we do not get a real root from x² + 1  as it is a complex root. So the only real root is x=1. If a polynomial equation has real coefficients, then either all roots are real or there are an even number of non-real complex roots, in pairs.

On the other hand, if the polynomial equation is not factorable, the roots can be determined from the graph by examining the x-intercepts. By graphing the function using a graphing calculator, you can get a sense of where the roots are and how many real roots exist when it crosses or touches the x-axis.


A set of functions with the same characteristics is a family of functions. When talking about a family of a polynomial function, we are talking about the general equation of the function. Polynomial functions that have the same x-intercepts belong to the same family.