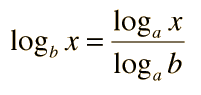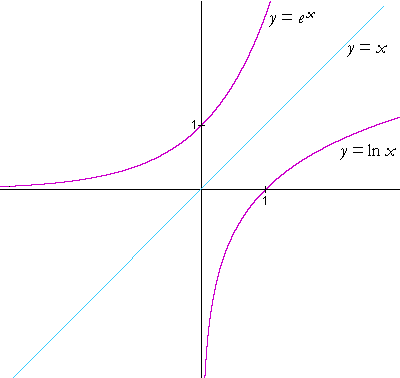Logarithmic Scales in Physical Sciences

Laws of Logarithms and Change of Base

Logarithm study has a few formulas that are important and key to solving math questions. By remembering them, you will be in line to solve logarithmic problems and, maybe, fast too. There are a few logarithms laws that are formed by combining two logs of the same base. 

• Product rule :  log(ab) = log(a) + log(b)
• Quotient rule : log(a/b) = log(a) - log(b)
• Power rule : log(xⁿ) = nlog(x)                     Ex: log₃9² = 2log₃9

If the logarithm to the base a is known, then the logarithm to the base b can be obtained by the base change relationship:

, b>0, b≠1, x>0

The base change formula helps in evaluating logarithms or graphing log functions with any base. For graphing, first find the inverse of the function in exponential form and draw its graph. To draw the graph of the function, reflect in the line y=x.

Transformations of Logarithmic Functions

Transformations apply to logarithmic functions the same way as they do to other functions. Recall what we have learnt in previous chapters on how transformations effect a function and its graph.

• f(x) → f(x) + c
• f(x) → f(x - d)
• f(x) → af(x)
• f(x) → f(kx)

The same techniques is applied to logarithmic functions. An equation of a transformed logarithmic function has a form of f(x) = a log_B [k (x+d)] + c where a, k, d and c are coefficients while B is the base of the log.

We must first apply the horizontal/vertical stretches or compressions first if any.

• y = log (kx) : Horizontal compression/stretch by factor of |1/k|
• y = a log x   : Vertical stretch/compression by a factor of |a|

The next step is to apply any reflections. If a <0, reflect in the x-axis. If k<0, reflect in the y-axis.

Then apply the horizontal or vertical translations to the function.

• y = f(x − d)  :  shift to the right by d units if d>0; translate left by d units if d<0
• y = log x + c : translate up by c units if c>0; shifts down by c units if c<0

Try answering these multiple choice questions on determining the shape of a graph when the logarithmic function is transformed. Hopefully it helps!

Logarithms

Logarithmic functions are the inverse of exponential functions.  For example, the inverse of y = a^x is y = log_ax, which is the same as x = a^y. For example, if (0, 1) is a point on the graph of an exponential function, then (1,0) would be the corresponding point on the graph of the inverse logarithmic function. This is proven in the graph below.

The graph of a logarithm function is a reflection of its exponential graph under the line y=x. 

• The domain is all real numbers and x>0. 
• The range is all real numbers with no restrictions. 
• has an x-intercept of 1 as it will always cross the x-axis a 1. The graph will never cross the y-axis because x can never equal 0.
• has a vertical asymptote at x=0 as the graph passes through the point (1,0)

Notice on the graph that, as x increases, y also increases. This means that the function is an increasing function. The graph is increasing as e > 1 but decreasing on its domain when 0 < e < 1.

Therefore, logarithm equations can be written in exponential form and vice versa. Sometimes, by changing everything in logarithmic form to exponential form, you can solve equations containing logarithms. The little chart below will hopefully help us remember how to convert from one to the other.