Logarithmic functions are the inverse of exponential functions. For example, the inverse of y = ax is y = logax, which is the same as x = ay. For example, if (0, 1) is a point on the graph of an exponential function, then (1,0) would be the corresponding point on the graph of the inverse logarithmic function. This is proven in the graph below.
The graph of a logarithm function is a reflection of its exponential graph under the line y=x.
- The domain is all real numbers and x>0.
- The range is all real numbers with no restrictions.
- has an x-intercept of 1 as it will always cross the x-axis a 1. The graph will never cross the y-axis because x can never equal 0.
- has a vertical asymptote at x=0 as the graph passes through the point (1,0)
Therefore, logarithm equations can be written in exponential form and vice versa. Sometimes, by changing everything in logarithmic form to exponential form, you can solve equations containing logarithms. The little chart below will hopefully help us remember how to convert from one to the other.
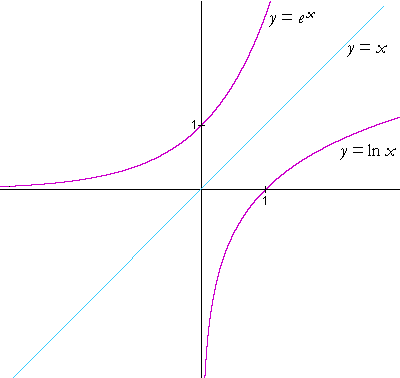

No comments:
Post a Comment